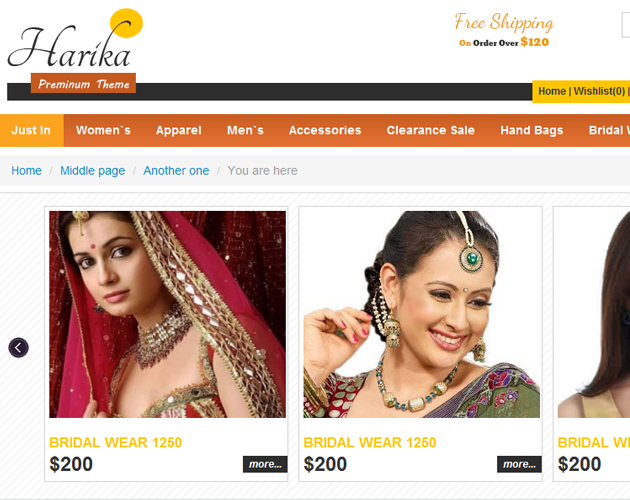
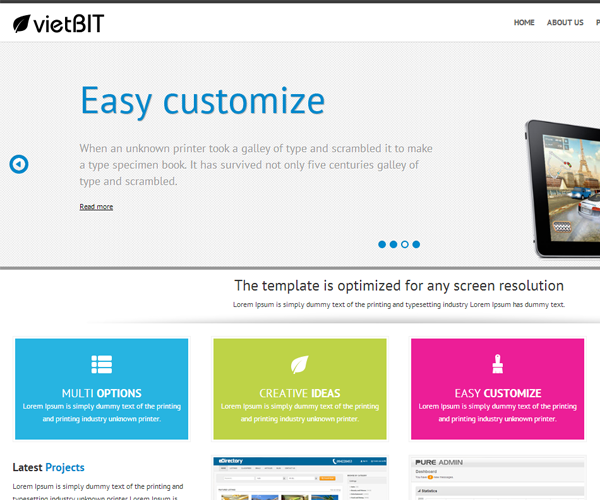
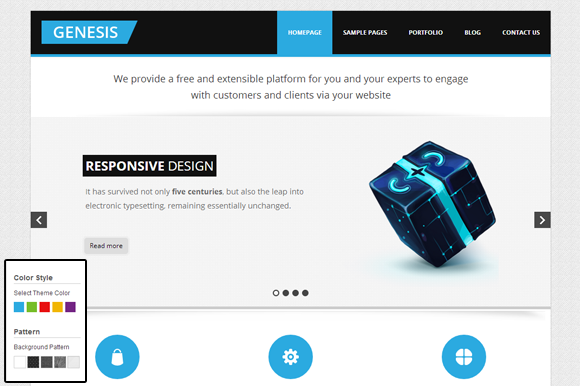
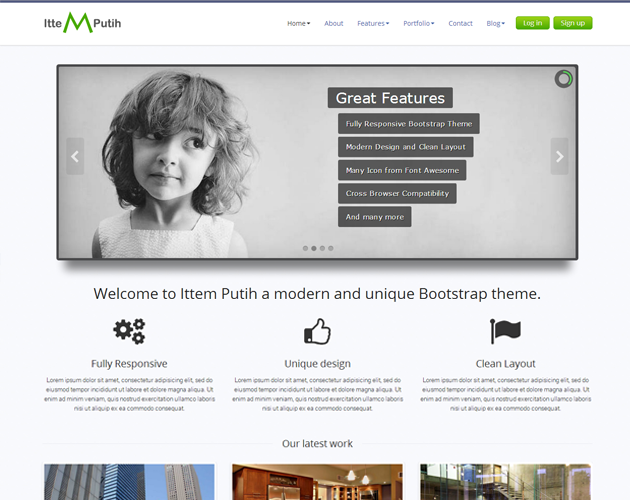
-
Boot Business$10 Downloads : 1
-
Tuner Admin
It resembles an admin panel. It could be your router admin panel where you can enter de default IP address of your router. The most common router IP address is 192.168.1.1, It is used by the most router brands.
$6 Downloads : 3 -
Elaine Business Template$6 Downloads : 18
-
ManiaAdmin - Responsive Admin Theme$12 Downloads : 2
-
Bootstrap E-Commerce Template$8 Downloads : 4
-
vietBIT - Responsive template$18 Downloads : 4
-
Genesis - Responsive template$16 Downloads : 1
-
Ittem Putih Responsive Template$10 Downloads : 8
-
Cap Admin - Responsive Admin Template$16 Downloads : 3
-
Braintag - Fully Responsive Theme$4 Downloads : 3
-
MyResume$6 Downloads : 1
-
Coolors Admin Dashboard$6 Downloads : 5